DEV

HyperLogLog 원리

HyperLogLog 자료구조에 대해 공부하면서 redis 소스 까보기

jiheon2234

— 7 min read
HyperLogLog 원리

Intro

데이터셋에서 고유 원소가 몇 개인지 알고 싶다면, 대개 Set이 떠오르죠.
삽입·조회가 거의 O(1)에 가깝고, 집합 그 자체니깐요.

그런데 Set은 해시 값과 원본 값을 둘 다 들고 있어서
원소가 많아질수록 메모리를 끝도 없이 잡아먹어요.
그럼 거의 정확히 고유 개수를 세면서도 메모리를 아낄 수 있을까요?

바로 여기서 HyperLogLog가 등장해요. (줄여서 HLL!)
HLL은 카디널리티를 추정하는 확률적 자료 구조인데,
정확도를 살짝 희생해서 공간(메모리)을 효율적으로 활용할 수 있어요.

이번 글에서는 HLL의 개념을 살펴보고, 실제 redis 소스를 통해 동작 원리를 파헤쳐 볼게요.

HLL 간단 개념

특정 원소를 64비트로 해싱했는데, 앞의 25 비트가 모두 0이라고 생각해보죠.

비트가 0일 확률은 ½, 25 개가 연속으로 0일 확률은 $2^{-25}$로 상당히 희귀한 패턴인데, 이런 희귀한 패턴이 나왔다면 그 전에 $2^{25}$개 정도의 원소가 있었다고 짐작할 수 있겠죠?

HLL은 바로 이 연속된 0의 길이(p)와 데이터 규모의 관계를 이용해 집합 크기를 추정하고 있는데, 아직 먼소린지 감이 안오니깐, 더 깊게 파보죠!

HLL 상세

struct

Hll 헤더 구조체는 다음과 같이 이루어져 있어요:

struct hllhdr {
    char    magic[4];   /* 식별용 시그니처: "HYLL"            */
    uint8_t encoding;   /* HLL_DENSE 또는 HLL_SPARSE          */
    uint8_t notused[3]; /* 예약 필드, 항상 0                  */
    uint8_t card[8];    /* 캐시된 카디널리티(LE)              */
    uint8_t registers[];/* 레지스터 데이터 (2^14 = 16384)       */
};

unit8_t registers[] 배열이 눈에 띄는데, redis에서는 16384의 기본 길이를 가지고 있어요. 각각의 공간에는 위에서 언급한 “가장 긴 연속된 0의 길이”가 저장되며, 이를 토대로 전체 카디널리티를 추정하죠.

hllPatLen()

요소를 해싱하고, 그 값으로 저장될 register의 인덱스와 연속된 0의 개수를 구하는 함수에요.

int hllPatLen(unsigned char *ele, size_t elesize, long *regp) {
    uint64_t hash, index;
    int count;
    hash = MurmurHash64A(ele,elesize,0xadc83b19ULL); /* 64비트 해시 생성 */
    index = hash & 0b11111111111111; /* LSB 하위 14비트 추출 */
    hash >>= HLL_P; /* 하위 14비트 제거 (HLL_P = 14) */
    hash |= ((uint64_t)1<<50);   /* 최상위비트 1로세팅(0일경우 대비) */

    count = __builtin_ctzll(hash) + 1; /* LSB부터 연속된 0의 개수 +1 */ 
    *regp = (int) index;
    return count;
}

그림으로도 정리해봤어요:

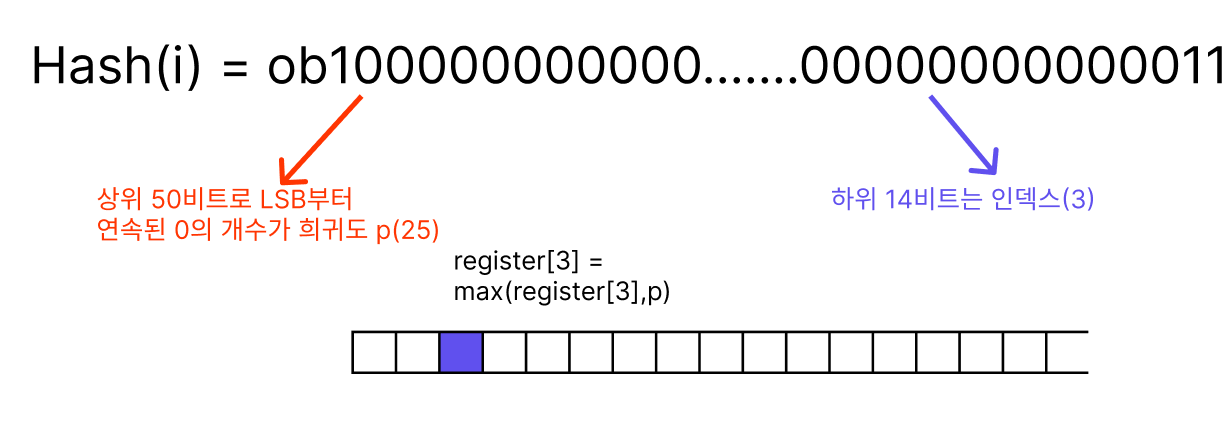
동작순서를 정리하면:

  1. 64비트 해싱
  2. 인덱스 결정: 해시 하위 14비트를 잘라서 인덱스로 사용
  3. 희귀도 계산: 남은 50비트에서 LSB부터 0이 몇 번 연속됐는지+1
  4. 인덱스와 희귀도 반환

hllAdd()

말 그대로 hll에 요소 하나를 추가하는 함수에요

int hllDenseAdd(uint8_t *registers, unsigned char *ele, size_t elesize) {
    long index;
    uint8_t count = hllPatLen(ele,elesize,&index); /* 인덱스, 희귀도 */
    return hllDenseSet(registers,index,count);
}

/* 해당 인덱스의 registers에 저장된  count와 비교하여
 * 더 크면 업데이트  */
int hllDenseSet(uint8_t *registers, long index, uint8_t count) {
    uint8_t oldcount;
    HLL_DENSE_GET_REGISTER(oldcount,registers,index);
    if (count > oldcount) {
        HLL_DENSE_SET_REGISTER(registers,index,count);
        return 1;
    } else {
        return 0;
    }
}

hllPatLen() 함수를 통해 얻은 인덱스와 희귀도를 통해, registers[index]에 가장 희귀한 값을 저장해요.

HLL 상세-개수 추정

이제, hll의 핵심인 실제 개수를 추정하는 로직을 살펴보죠.

uint64_t hllCount(struct hllhdr *hdr, int *invalid) {
    double m = HLL_REGISTERS;  /* 16384 */
    double E;
    int j;

		/* 레지스터 분포 히스토그램 만들기
   	 * reghisto[ρ] == ρ(0‥63) 값을 가진 레지스터의 개수
		 */
    int reghisto[64] = {0};
    hllDenseRegHisto(hdr->registers,reghisto);

     /* ρ ≥ 51(overflow) 보정: τ(x) */
    double z = m * hllTau((m-reghisto[HLL_Q+1])/(double)m);
    
    /* ③ 중간 구간 누적  
		 *  HLL_Q = 50,  ρ = Q‥1까지 Σ 2⁻ρ 를 재귀적으로 계산. */
    for (j = HLL_Q; j >= 1; --j) {
        z += reghisto[j];
        z *= 0.5;
    }
    
    /* ④ Small-range 보정: σ(x)
		 * ρ = 0(빈 레지스터)이 많을 때 생기는 편향 보정. */
    z += m * hllSigma(reghisto[0]/(double)m);
    
    /* ⑤ 최종 추정치
     * 	HLL_ALPHA_INF ≈ 0.7213
		 *    E = α∞ · m² / z  */
    E = llroundl(HLL_ALPHA_INF*m*m/z);

    return (uint64_t) E;
}

먼저, hllDenseRegHisto() 함수는 각 register의 연속된 0의 개수(p)를 인덱스로 가지는 히스토그램을 만들어요.
나머지는 HyperLogLog 공식인데, Hll논문을 코드로 옮긴 거에요

간단한 개요만 설명하면:

  1. hllTau(**)** 함수로 p가 51이상일 경우 보정,
  2. ρ = 50→1까지 Σ 2⁻ρ 계산 $Z = \left( \sum_{j=1}^{m} 2^{-R_j} \right)^{-1}$
  3. hllSigma() 함수로, 빈 레지스터 비율에 따른 편향 보정.
  4. α∞·m² / Z 스케일링으로 카디널리티 수정.

왜 오차가 이렇게 작을까?

통계학에는 "표본(sample)의 개수가 많아질수록 그 평균은 실제 모집단의 평균에 가까워진다"는 대수의 법칙이 존재해요.

HLL은 요소의 해시의 앞선 14비트를 통해 16,384개의 레지스터 중 어디에 저장할지를 결정하고, 나머지 50비트를 통해 p를 계산하는데, 몇몇 레지스터에서 우연히 높은 p가 나와도, 나머지 레지스터가 평균(조화평균)을 내면서 그 영향을 상쇄시키는 거에요.

반대로 표본이 너무 적으면 대수의 법칙이 제대로 작동하지 않아 추정 오차가 커지게 되요. (redis에서는 표본이 별로 없는 초기엔 헤더가 HLL_SPARSE로 인코딩되어 다른 메커니즘으로 동작해요)
또한, HLL은 “해시 값이 균등하게 분포한다” 는 가정 위에 세워진 알고리즘이라, 해시함수의 편향에 따라 추정치가 크게 왜곡될 수 있어요.

Final

HyperLogLog는 set과 달리 작은 고정 메모리로도 카디널리티를 거의 정확하게 집계할 수 있는 훌륭한 도구에요. 다만 절대적인 정확도가 필요하거나, in ,del등의 다른 집합 연산이 필요한 경우엔 사용할 수 없죠.

사실 이 포스팅을 작성하면서 redis의 hyperloglog.c를 뜯어봤는데, 제가 지금 포스팅한 건 정말 빙산의 일각에 불과해요. n이 작을때 작동하는 sparse 메커니즘과 dense로의 promote, registers에 저장되는 p는 최대 50이라 사용되는 6비트 패킹, Σ 2⁻ρ 최적화, pfmergeCommand, 논문의 보정 공식 …. 실제로 redis HLL을 쓰면서는 굳이 알 필요 없는 것들이지만, 오픈소스 내부를 직접 따라가 본 것에 의미를 두려고 해요.

3-point

  1. HLL는 적은 메모리로 집합의 카디널리티를 근사 추정할 수 있는 확률적 자료구조다.
  2. 실제 코드를 뜯어보면 지독하게 최적화되어 있다.
  3. 나는 수학이 싫다.

Read more