DEV

Bloom Filter 원리

Bloom filter 내부 동작 원리에 대해 알아보자. (feat. redis)

jiheon2234

— 7 min read
Bloom Filter 원리

Intro

Bloom Filter(BF)는 “특정 원소가 집합에 존재하는지” 여부를 효율적으로 검사하는 확률적 자료구조에요. HyperLogLog 처럼 Set의 메모리 부담을 줄이도록 설계되었으며 HLL이 카디널리티 추정에 특화되었다면, BF는 집합의 포함 여부 (in)에 특화되어 있죠.

물론 확률적 자료구조인 만큼 100% 정확하진 않지만, 최소한 있는 걸 없다고 하진 않아요.

이제부터 BF의 개념과 동작 원리에 대해 살펴볼게요.

BF 구조

Redis에서 BF는 다음과 같이 구현되어 있어요.

struct bloom {
    uint32_t hashes;     // 해시 함수 개수
    uint8_t force64;     // 64비트 강제 여부
    uint8_t n2;          // 비트맵 크기를 2^n으로 표현할 때의 n (n2)
    uint64_t entries;    // 예상 삽입 개수

    double error;        //  허용 오차율
    double bpe;          // 비트 수 / 원소 수 (bits per element)

    unsigned char *bf;   // 비트맵 포인터
    uint64_t bytes;      // 비트맵 바이트 수
    uint64_t bits;       // 비트맵 비트 수
};

원본

간단하게 말해, 다음과 같은 비트 배열이라고 생각하면 돼요:

BF 동작원리

Insert

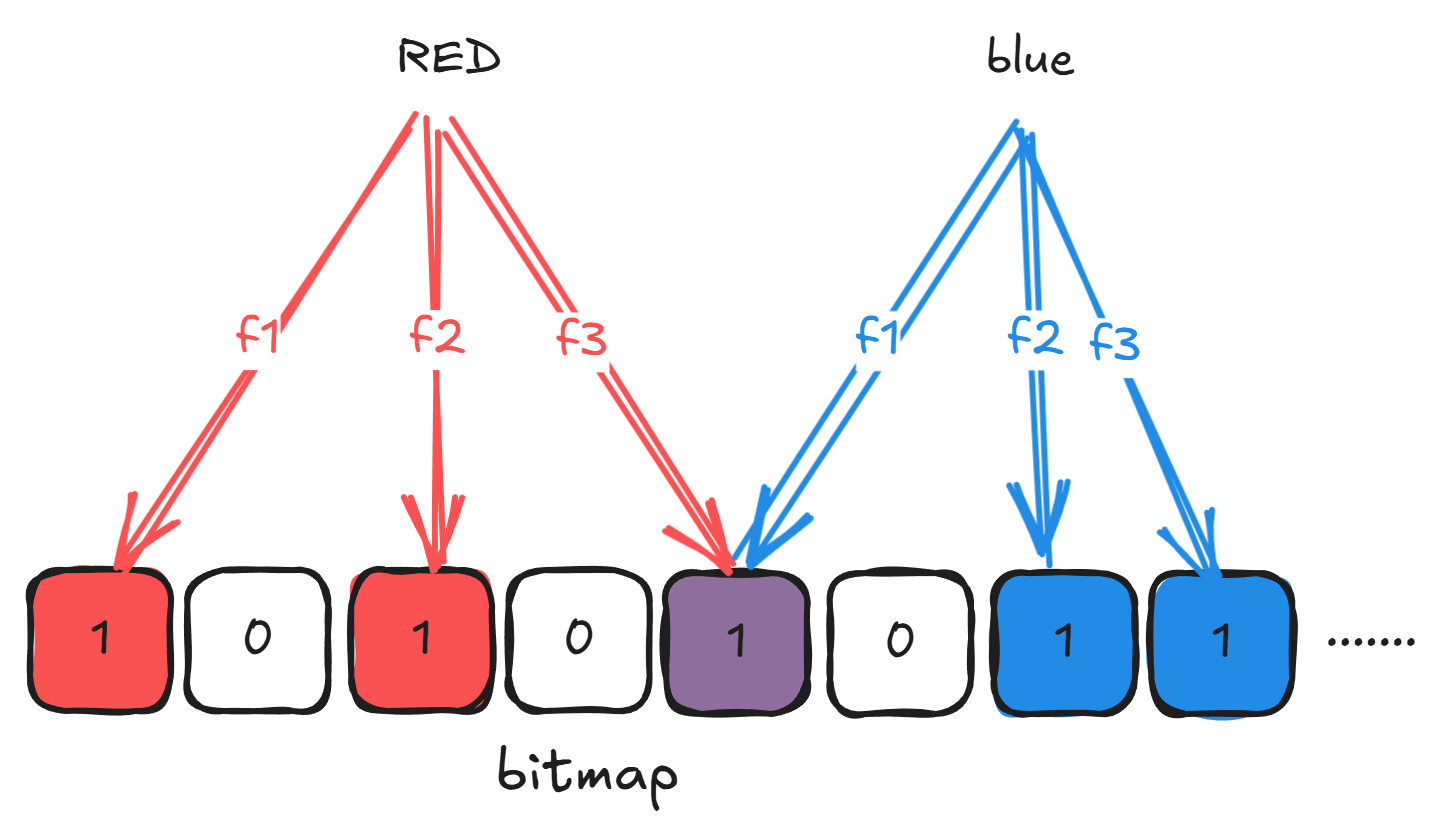
어떤 원소를 BF에 추가하는 과정은 다음과 같아요:

  1. n개의 해시 함수로 n개의 비트 인덱스를 계산하고
  2. 비트맵에서 해당 인덱스의 비트들을 1로 마킹해요.

find

특정 원소를 찾는 과정은 원소 추가 과정과 비슷해요.

  1. n개의 해시 함수를 통해 n개의 인덱스를 결정하고
  2. 비트맵에서 해당 인덱스들이 전부 1인지 검사해요.

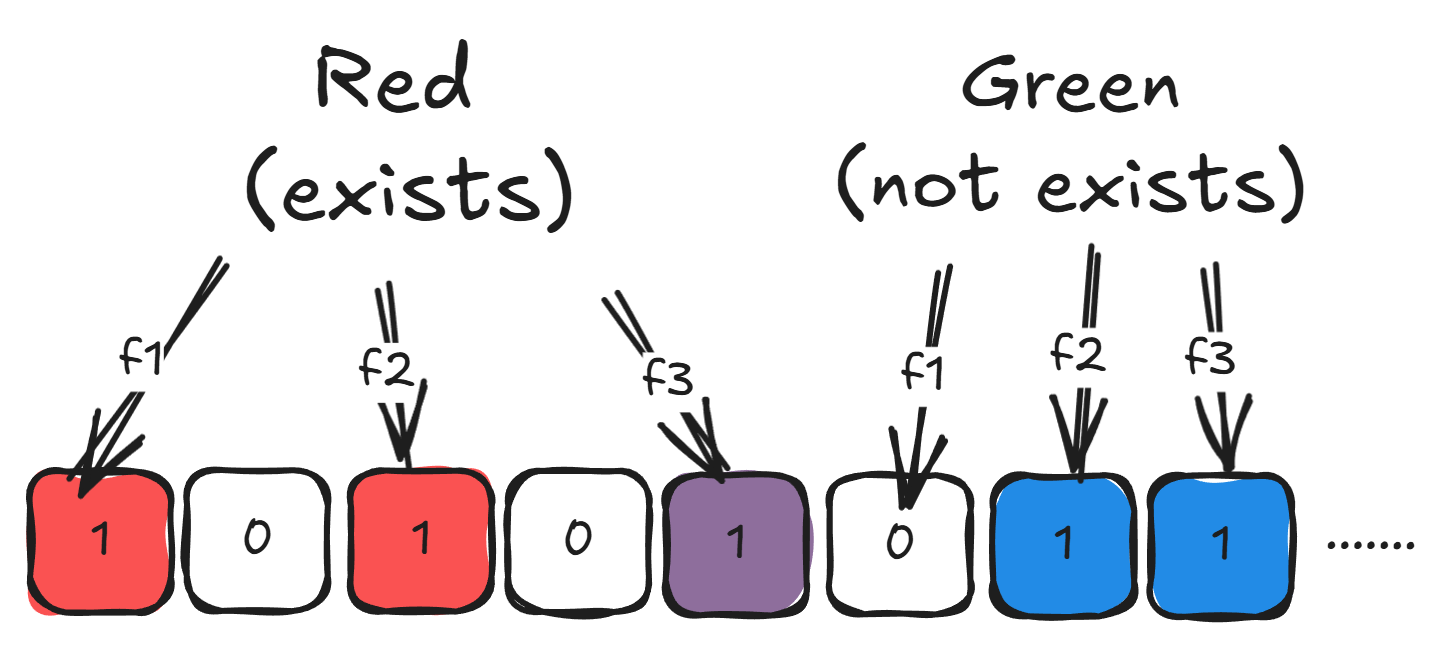
실제로 존재하는 원소라면, 당연히 해당 비트가 전부 1이니깐 있다고 판단하겠죠.

그런데 BF에 없는 원소를 해싱했을 때 나오는 n개의 인덱스가, 이미 다른 원소들에 의해 전부 마킹되었으면 어떻게 될까요?

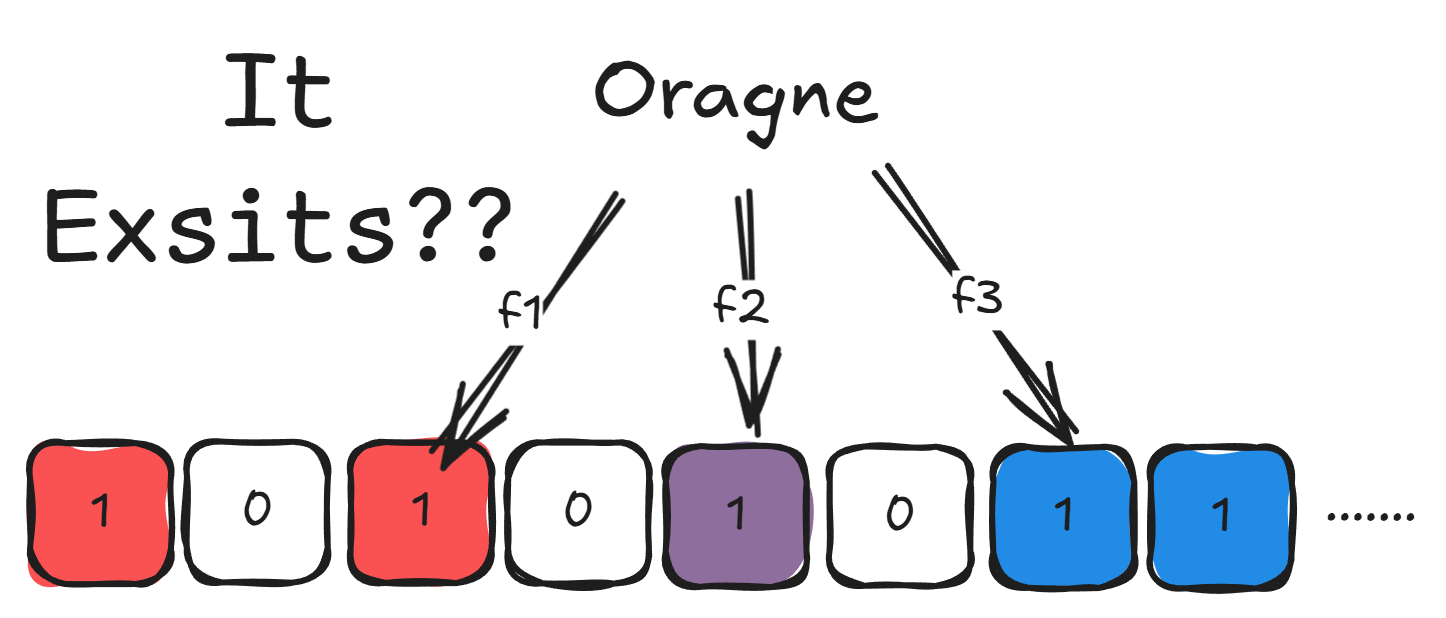
현재 비트맵에는 red와 blue만 있지만, orange의 인덱스들도 전부 1이므로 BF는 orange가 있다고 대답할 거예요.

이걸 “false positive(거짓 긍정)”이라고 해요.

삭제 불가능

BF에서는 원소 삭제가 불가능해요.

특정 원소를 해싱해서 비트맵의 인덱스까지는 구한다 해도, 각 인덱스들이 얼마나 많은 원소들에 의해 마킹됐는지 알 수 없죠.

이걸 무시하고 해당 인덱스를 0으로 마킹하는 순간, 해당 인덱스를 사용하던 다른 원소들까지 삭제될 거에요.

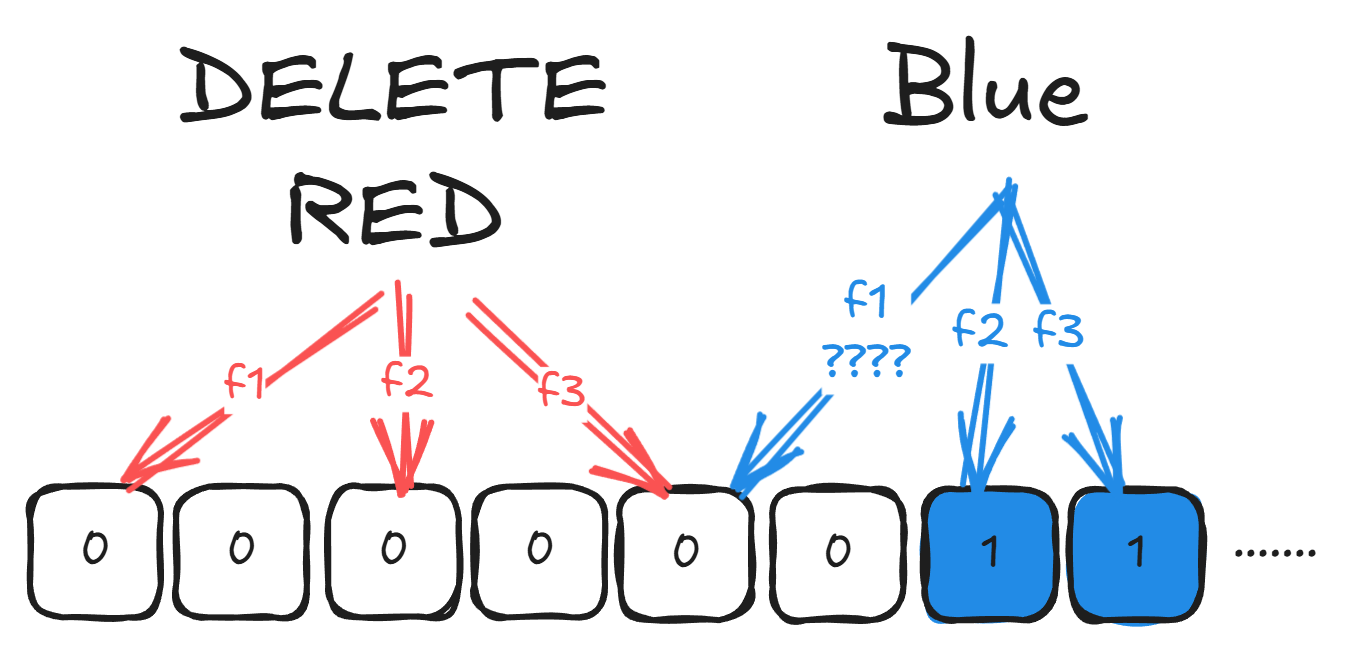
즉, BF에서는 한 번 마킹된 비트는 절대 되돌릴 수 없어요.

이 단점을 보완하기 위해 삭제가 가능한 Counting Bloom Filter, Cuckoo Filter 등이 등장했어요.

TMI

Scalable

기본적으로 BF는 확장이 불가능한 구조이지만, redis에서는 여러 BF를 체인으로 엮는 SBChain 구조를 사용하기 때문에 필터가 가득 찼을 때 새로운 필터가 추가하면서 자동으로 확장돼요. 생성시에 BF.RESERVE {key} {error_rate} {capacity} NONSCALING으로 이를 비활성화 할 수 있어요.

hash function

지금까지 BF에서 여러개의 해시함수를 사용한다고 설명했지만, Redis에선 MurmurHash2 하나만 사용해요. 정확히는, MurmurHash2함수를 두 번 호출하여 초기 해시값 a,b 을 계산하고, T x = ((hashval.a + i * hashval.b)) % mod 를 사용하여 여러 해시 인덱스를 계산해요. 이런 방식을 Double Hashing 이라고 불러요.

오차율

BF의 오차율은 앞서 설명한 false positive 가 생길 확률을 말하는데, 공식은 다음과 같아요:

$$ P = \left(1 - \left(1 - \frac{1}{m} \right)^{kn} \right)^k $$

$$ P \approx \left(1 - e^{-kn/m} \right)^k$$

*P: 오차율m: 비트맵 비트 수n: 삽입된 원소 수 k: 해시 함수 개수*

각 해시가 특정 비트 하나를 선택하지 않을 확률은 $1 - \frac{1}{m}$, 이걸 k*n번 반복하면 $\left(1 - \frac{1}{m} \right)^{kn}$,
따라서, 한번이라도 선택될 확률은 $\left(1 - \frac{1}{m} \right)^{kn}$이고, 그럼 $k$개의 해시로 검사했을 때 모든 해시 인덱스가 1로 설정될 확률은 $\left(1 - \left(1 - \frac{1}{m} \right)^{kn} \right)^k$,

여기서 n이 크다면 $\left(1 - e^{-kn/m} \right)^k$로 근사하는 거죠.

redis에서 BF를 생성할 때 BF.RESERVE <key> <error_rate> <capacity> 명령어를 사용하는데, 이때 전달된 오차율과 용량을 통해 내부적으로 최적의 비트맵 크기와 해시 함수의 개수를 자동으로 계산해줘요.

n2

비트맵의 비트 수는 기본적으로 2ⁿ 인데, 여기엔 재미있는 이유가 있어요. 64비트 해시를 비트맵의 인덱스에 맞추기 위해선 mod 연산이 필요한데, 이 mod는 상당히 비싼 연산이에요.

하지만 분모가 2ⁿ임이 확실하면, 컴파일러는 % 대신 hash & ((1 << n) - 1) 같은 가벼운 비트 AND 연산으로 자동 치환할 수 있어요.

실제 코드에서도 << 를 이용해서, 이 값은 2ⁿ임을 알려주고 있죠.

static int bloom_check_add64(struct bloom *bloom, bloom_hashval hashval, int mode) {
    CHECK_ADD_FUNC(uint64_t, (1LLU << bloom->n2));
}

Final

BF는 대용량 데이터를 다룰 때, 집합에 원소가 존재하는지를 메모리 효율적으로 판단할 수 있어요. 다만 확률적 자료 구조인 만큼 false positive의 가능성이 있다는 것과, 삭제가 불가능하다는 것을 염두에 두고 사용해야 해요.

즉, 단독으로 사용하기보단 전처리 필터로 사용한다던지, 아니면 “존재하지 않음”만 판단할 수 있는 상황에 딱 맞는 거죠. 대표적으로:

  • 사용자의 광고 중복 노출을 방지
  • 존재하지 않는 키로 인한 캐시 미스 방지

등이 있겠네요.

다만, 조금의 오류도 허용해선 안 되는 경우엔 BF를 사용할 수 없겠죠?

3-point

  1. BF는 메모리 효율적으로 집합에 원소가 있는지 확인하는 확률적 자료구조이다.
  2. 거짓 긍정은 발생할 수 있으며, 거짓 부정은 발생하지 않는다. 삭제는 불가능하다.
  3. 나는 수학이 싫다.

Read more